This article is the third part in a miniseries on building a project cost duration graph. The first part can be found here and the second part here. If you have already read them please ignore this paragraph. If not I would encourage you to read them first as they will provide you with a more comprehensive understanding of the subject.
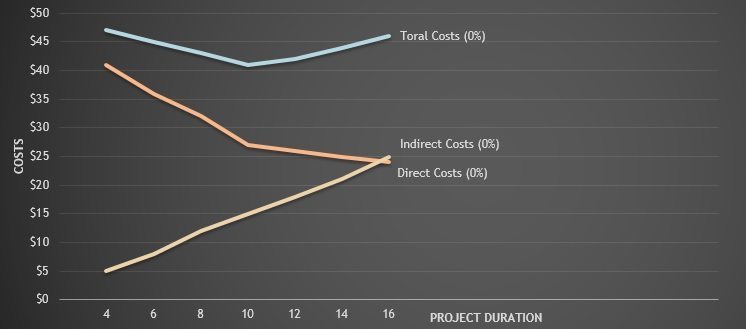
This cost duration graph, as presented in the figure below, is valuable to compare any proposed alternative or change with the optimum cost and time.
More importantly the creation of such a graph keeps the importance of indirect costs in the forefront of decision making. Indirect costs are frequently forgotten in the field when the pressure for action is intense. Finally, a cost duration graph can be used before the project begins or while the project is in progress.
- Creating the cost duration graph in the project planning phase without an imposed duration is the first choice because normal time is more meaningful.
- Creating the cost duration graph in the project planning phase with an imposed duration is less desirable because normal time is made to fit the imposed date and is probably not low cost.
- Creating the cost duration graph after the project has started is the least desirable because some alternatives may be ruled out of the decision process. Managers may choose not to use the formal procedure demonstrated.
However, regardless of the method used, the principles and concepts inherent in the formal procedure are highly applicable in practice and should be considered in any cost—duration trade-off decision.
Project Cost Duration Graph Methods
Crash Times
Collecting crash times for even a moderate-size project can be difficult. The meaning of crash time is difficult to communicate. What is meant when you define crash time as “the shortest time you can realistically complete an activity”?
Crash time is open to different interpretations and judgments. Some estimators feel very uncomfortable providing crash times. Regardless of the comfort level, the accuracy of crash times and costs is frequently rough at best, when compared with normal time and cost.
Linearity Assumption
Because the accuracy of compressed activity times and costs is questionable, the concern of some theorists—that the relationship between cost and time is not linear but curvilinear—is seldom a concern for practicing managers. Reasonable, quick comparisons can be made using the linear assumption. The simple approach is adequate for most projects. There are rare situations in which activities cannot be crashed by single time units. Instead, crashing is “all or nothing.”
For example, activity A will take 10 days (for say $1,000) or it will take 7 days (for say $1 , 500), but no options exist in which activity A will take 8 or 9 days to complete. In a few rare cases of very large, complex, long-duration projects, the use of present value techniques may be useful; such techniques are beyond the scope of this text.
Activities to Crash
The cost—time crashing method relies on choosing the cheapest method for reducing the duration of the project. There are other factors that should be assessed beyond simply cost.
First, the inherent risks involved in crashing particular activities need to be considered. Some activities are riskier to crash than others.
For example, accelerating the completion of a software design code may not be wise if it increases the likelihood of errors surfacing downstream. Conversely, crashing a more expensive activity may be wise if fewer inherent risks are involved.
Second, the timing of activities needs to be considered. Crashing an early activity may be prudent if there is concern that subsequent activities are likely to be delayed, and absorb the time gained. Then the manager would still have the option of crashing final activities to get back on schedule.
Third, crashing frequently results in overallocation of resources. The resources required to accelerate a cheaper activity may suddenly not be available. Resource availability, not cost, may dictate which activities are crashed.
Finally, the impact crashing would have on the morale and motivation of the project team needs to be assessed. If the least-cost method repeatedly signals a subgroup to accelerate progress, fatigue and resentment may set in. Conversely, if overtime pay is involved, other team members may resent not having access to this benefit. This situation can lead to tension within the entire project team. Good project managers gauge the response that crashing activities will have on the entire project team.
Time Reduction Decisions and Sensitivity
Should the project owner or project manager go for the optimum cost-time? The answer is, “It depends.” Risk must be considered. The project direct-cost line near the normal point is usually relatively flat.
Because indirect costs for the project are usually greater in the same range, the optimum cost-time point is less than the normal time point. Logic of the cost-time procedure suggests managers should reduce the project duration to the lowest total cost point and duration.
Cost Duration Graph For Projects With Several Critical or Near-Critical Paths
How far to reduce the project time from the normal time toward the optimum depends on the sensitivity of the project network. A network is sensitive if it has several critical or near-critical paths. Project movement toward the optimum time requires spending money to reduce critical activities, resulting in slack reduction and/or more critical paths and activities. Slack reduction in a project with several near-critical paths increases the risk of being late.
The practical outcome can be a higher total project cost if some near-critical activities are delayed and become critical; the money spent reducing activities on the original critical path would be wasted. Sensitive networks require careful analysis.
The bottom line is that compression of projects with several near-critical paths reduces scheduling flexibility and increases the risk of delaying the project. The outcome of such analysis will probably suggest only a partial movement from the normal time toward the optimum time.
Cost Duration Graph For Projects With One Dominant Critical Path
There is a positive situation where moving toward the optimum time can result in very real, large savings—this occurs when the network is insensitive. A project network is insensitive if it has a dominant critical path, that is, no near-critical paths. In this project circumstance, movement from the normal time point toward the optimum time will not create new or near-critical activities.
The bottom line here is that the reduction of the slack of noncritical activities increases the risk of their becoming critical only slightly when compared with the effect in a sensitive network. Insensitive networks hold the greatest potential for real, sometimes large, savings in total project costs with a minimum risk of noncritical activities becoming critical.
Insensitive networks are not a rarity in practice; they occur in perhaps 25 percent of all projects.
For example, a light rail project team observed from their network a dominant critical path and relatively high indirect costs. It soon became clear that by spending some dollars on a few critical activities, very large savings of indirect costs could be realized. Savings of several million dollars were spent extending the rail line and adding another station.
The logic found in this example is just as applicable to small projects as large ones. Insensitive networks with high indirect costs can produce large savings.
Ultimately, deciding if and which activities to crash is a judgment call requiring careful consideration of the options available, the costs and risks involved, and the importance of meeting a deadline.